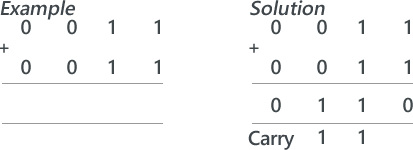Binary Addition
In this lesson, students will learn how to add two 8‐bit binary integers and explain overflow errors which may occur.
Learning Objectives:
Suggested time: 50 mins
Curriculum Mapping:
Learning Objectives:
- add two 8‐bit binary integers and explain overflow errors which may occur
Suggested time: 50 mins
Curriculum Mapping:
KS3:
- Understand how data of various types (including text, sounds and pictures) can be represented and manipulated digitally, in the form of binary digits
COMPUTER SCIENCE EDUCATORS:
1a: Demonstrate knowledge of and proficiency in data representation and abstraction
- Effectively use primitive data types
- Demonstrate an understanding of static and dynamic data structures
- Effectively use, manipulate and explain various external data stores: various types (text, images, sound, etc.), various locations (local, server, cloud), etc.
- Effectively use modeling and simulation to solve real-world problems
CSTA K–12 CS Standards:
- 2-DA-07: Represent data using multiple encoding schemes.
- 3A-DA-09: Translate between different bit representations of real-world phenomena, such as characters, numbers, and images.
Lesson 1: Theory (Binary Addition)
Starter:
Start with this fun starter activity courtesy of Mark Ward via CAS called Binary Bingo. To download the activity, click here.
Give each student a bingo card and pick numbers at random using a free random name selector (see Classroom Management Tools). The first student to get a full house is the winner.
Main:
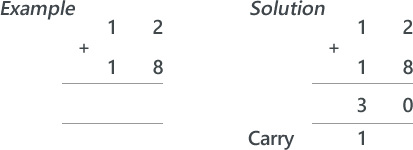
Begin by writing a simple sum (adding to denary numbers together) on the board:
Starter:
Start with this fun starter activity courtesy of Mark Ward via CAS called Binary Bingo. To download the activity, click here.
Give each student a bingo card and pick numbers at random using a free random name selector (see Classroom Management Tools). The first student to get a full house is the winner.
Main:
Begin by writing a simple sum (adding to denary numbers together) on the board:
Ask for a volunteer to solve it (showing all working out).
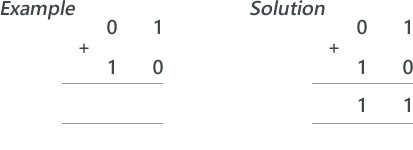
Next, introduce a simple binary sum:
Next, introduce a simple binary sum:
Explain that adding binary numbers is exactly the same as adding denary numbers however, instead of carrying groups of ten, you carry groups of 2. Follow this by writing a couple more simple binary sums on the board and ask for volunteers to attempt to solve these.
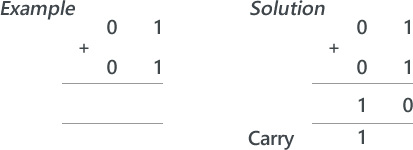
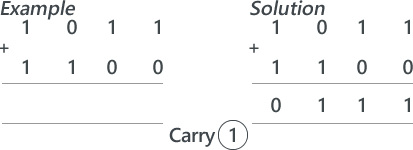
Next, explain that when we add two 1s we need to carry over to the next column. Demonstrate this using the following sum:
Next, explain that when we add two 1s we need to carry over to the next column. Demonstrate this using the following sum:
Follow this by asking students to work out the following (explaining their working out):
Finally, write the following binary sum on the board and ask the students to solve it. Ask students to identify the problem.
Explain that, if we only have 4 bits to store the result, there would be no room for the final carry – resulting in the wrong answer. Explain that when there isn’t room to store the resulting calculation, we get an error which we call overflow.
Finally, give students a series of binary addition challenges courtesy of Chris Barnard via CAS. You can download the worksheet and answer sheet here: Binary Addition Exercise
Extension:
Direct students to the following YouTube video explaining binary subtraction:
Finally, give students a series of binary addition challenges courtesy of Chris Barnard via CAS. You can download the worksheet and answer sheet here: Binary Addition Exercise
Extension:
Direct students to the following YouTube video explaining binary subtraction:
Plenary:
Ask students to play the CISCO Binary Game: http://forums.cisco.com/CertCom/game/binary_game_page.htm
Resources:
Useful resources:
Binary Calculator – http://gwydir.demon.co.uk/jo/numbers/binary/add.htm
Binary Arithmetic Task - http://www.allaboutcircuits.com/worksheets/bin_math.html
Ask students to play the CISCO Binary Game: http://forums.cisco.com/CertCom/game/binary_game_page.htm
Resources:
Useful resources:
Binary Calculator – http://gwydir.demon.co.uk/jo/numbers/binary/add.htm
Binary Arithmetic Task - http://www.allaboutcircuits.com/worksheets/bin_math.html
Tags: GCSE, KS4, Theory, Computing Theory, CS Theory, Binary, Binary Representation, binary 2, binary conversion, how to do binary conversion, counting binary, binary number to decimal, binary 101, 8 binary, binary digits, binary digit, meaning of binary