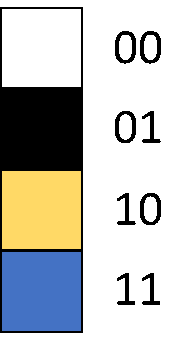Binary Lessons

Binary Representation of Images (Festive version)
In this lesson, students learn how a computer represents an image using binary.
For non-festive version, click here
Suggested time: 100 mins
Learning Objectives:
Curriculum Mapping:
In this lesson, students learn how a computer represents an image using binary.
For non-festive version, click here
Suggested time: 100 mins
Learning Objectives:
- Explain the representation of an image as a series of pixels represented in binary
- Explain the need for metadata to be included in the file such as height, width and colour depth
- Discuss the effect of colour depth and resolution on the size of an image file
Curriculum Mapping:
KS2 Computing:
- Use logical reasoning to explain how some simple algorithms work and to detect and correct errors in algorithms and programs → Students explore binary encoding and image representation, which involves logical reasoning and understanding simple data encoding algorithms.
- Use search technologies effectively; evaluate digital content; use technology safely and responsibly → The lesson introduces digital image formats and metadata, encouraging evaluation of digital content.
KS3 Computing:
- Understand the hardware and software components that make up computer systems, and how they communicate → The lesson explains how computers store and interpret image data using binary, linking to hardware/software interaction.
- Create and evaluate digital artefacts → Students create bitmap images and convert them to binary, fulfilling this requirement.
Digital Competence Framework:
- Citizenship: Identity, image, reputation, online behaviour, digital rights → The lesson touches on image creation and representation, which can be extended to discussions on digital identity and image use.
- Data & Computational Thinking: Data and information literacy → Core focus of the lesson: understanding how data (images) are represented and stored digitally.
- 1.2 Digital Citizen: Can be extended to include ethical use of digital images and privacy when sharing content.
- 1.3 Knowledge Constructor: Students evaluate how image resolution and colour depth affect file size and quality.
- 1.5c Computational Thinker: Students break down image representation into binary components and model bit-planes.
- 1.7 Global Collaborator: Group activities like the unplugged starter encourage collaboration and teamwork.
Algorithms and Programming (AP):
- 1B-AP-15: Test and debug a program or algorithm → Students convert images to binary and can test their representations for accuracy.
Impacts of Computing (IC):
- 2-IC-07: Compare positive and negative impacts of technology → Opportunity to discuss image compression and storage efficiency.
- 2-IC-08: Legal and ethical responsibilities of digital content → Can be extended to include copyright and ethical use of digital images.
- 3A-IC-11: Social and economic implications of digital privacy → Relevant if lesson includes discussion on metadata and image sharing.
- MS-ETS1-1: Define criteria and constraints of a design problem → Students design bitmap images within constraints of resolution and colour depth.
- HS-ETS1-3: Evaluate solutions to real-world problems → Students evaluate how binary representation affects image quality and file size.
- Science Practices: Analysing data, engaging in argument from evidence → Students analyse how bit-depth affects image representation and argue for optimal formats.
- Crosscutting Concepts: Cause and effect; systems and system models → Binary encoding as a system model for image representation.
- RI.6.8: Evaluate arguments and claims → Students discuss and evaluate claims about image quality vs. file size.
- RI.7.7: Compare text to multimedia versions → Students compare binary representations to visual images.
- W.8.1: Write arguments with evidence → Students can write about the effectiveness of different bit-depths in image encoding.
- SL.7.1: Engage in collaborative discussions → Group activities and peer review during bitmap creation and binary conversion.
Introduction: (Teacher guide)
Data in computers is stored and transmitted as a series of ones and zeros (also known as Binary).
To store an image on a computer, the image is broken down into tiny elements called pixels. A pixel (short for picture element) represents one colour. An image with a resolution of 1024 by 798 pixels has 1024 x 798 pixels (817,152 pixels).
In order for the computer to store the image, each pixel is represented by a binary value. We call this representation of colours a “bit-plane”. Each bit doubles the number of available colours i.e. 1-bit would give us 2 colours, 2-bits would give us 4 colours and 3-bits would give us 8 colours etc.
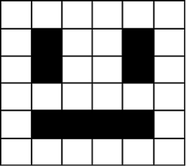
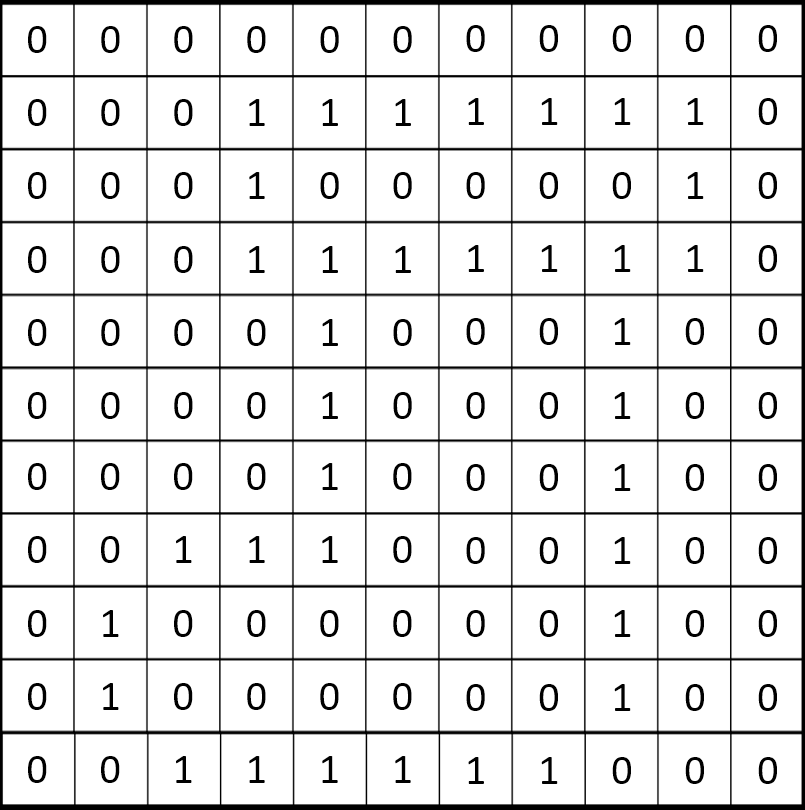
In a monochrome (two colour) image, like the example below, just 1 bit is needed to represent each pixel e.g. 0 for white and 1 for black.
Data in computers is stored and transmitted as a series of ones and zeros (also known as Binary).
To store an image on a computer, the image is broken down into tiny elements called pixels. A pixel (short for picture element) represents one colour. An image with a resolution of 1024 by 798 pixels has 1024 x 798 pixels (817,152 pixels).
In order for the computer to store the image, each pixel is represented by a binary value. We call this representation of colours a “bit-plane”. Each bit doubles the number of available colours i.e. 1-bit would give us 2 colours, 2-bits would give us 4 colours and 3-bits would give us 8 colours etc.
In a monochrome (two colour) image, like the example below, just 1 bit is needed to represent each pixel e.g. 0 for white and 1 for black.
Images are stored in scan lines. Each line is encoded from left to right, top to bottom. The image here would receive the following binary values:

000000
010010
010010
000000
011110
000000
010010
010010
000000
011110
000000
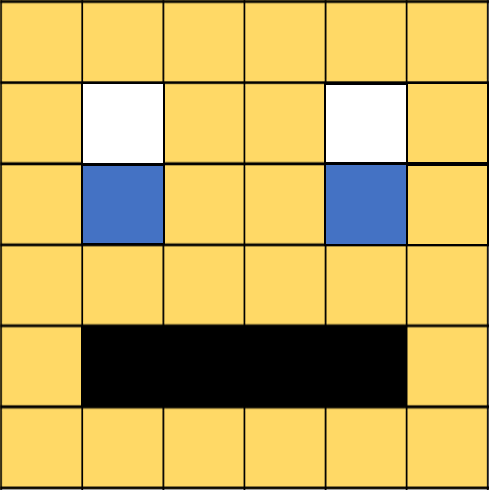
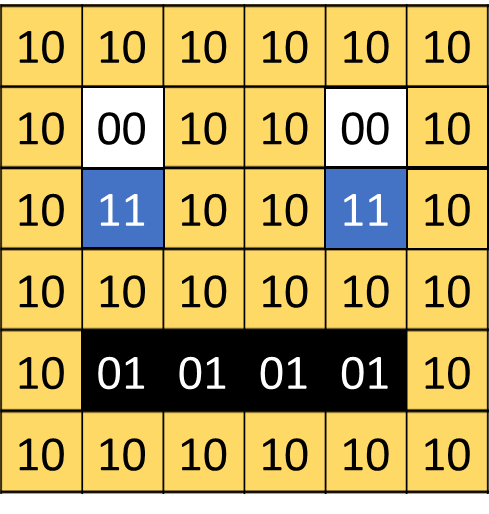
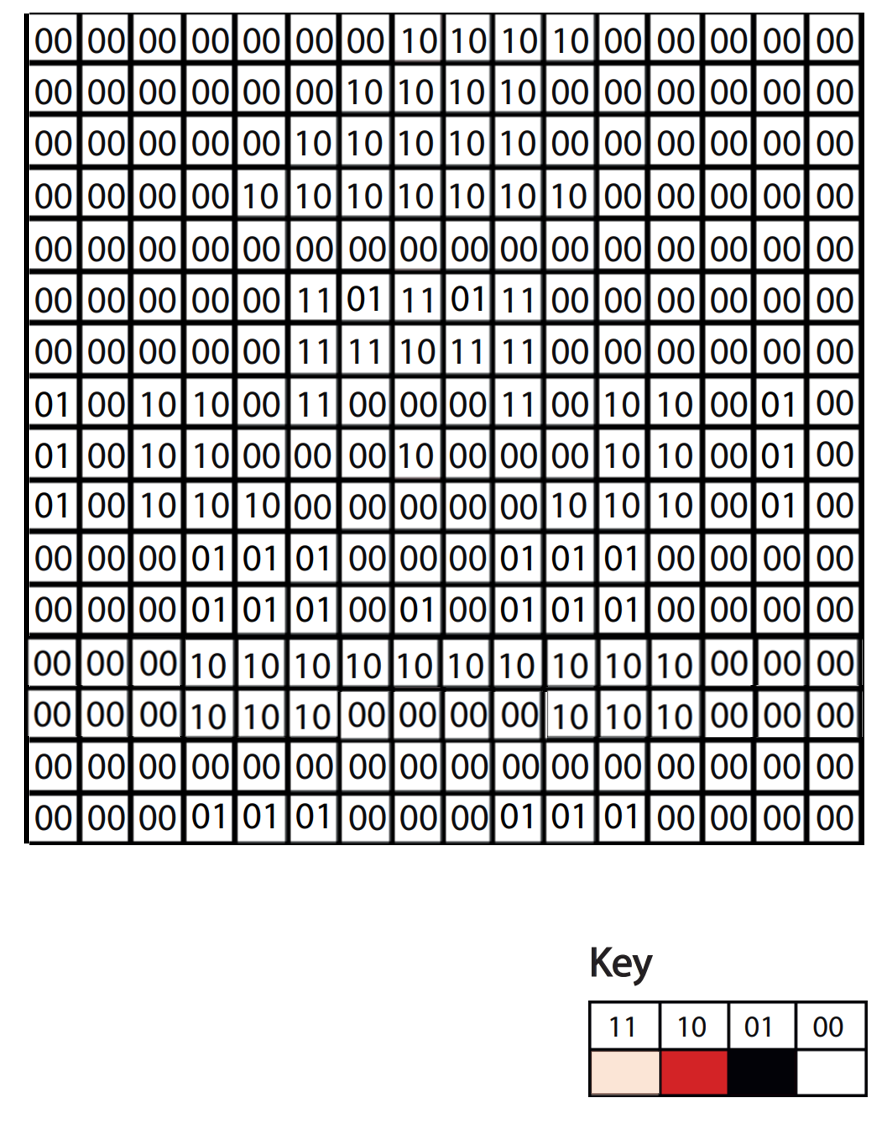
In an image that uses 4 colours, 2 bits are needed for each pixel. The following example uses two bits to store the following colours:
00 – White; 01 – Black; 10 – Yellow; 11 – Blue
00 – White; 01 – Black; 10 – Yellow; 11 – Blue
In order for the computer to interpret the image, the computer needs to know the following:
We call this extra piece of information “metadata”.
Want to know more?
To find out more about how a computer represents an image using binary, click on the links below:
- Colour depth – how many bits represent each pixel
- Resolution - Width & Height (in pixels)
We call this extra piece of information “metadata”.
Want to know more?
To find out more about how a computer represents an image using binary, click on the links below:
- GCSE Computing revision (Binary image representation) - https://mattg99.wordpress.com/2011/05/21/gcse-computing-revision-binary-image-representation/
- CS Unplugged (Image representation) https://csunplugged.org/image-representation
- BBC: Cracking the code (How pictures can be represented in the form of binary) - https://www.bbc.co.uk/programmes/p0166rgs
Lesson Outline:
In this lesson, students learn how a computer represents an image using binary.
In this lesson, students learn how a computer represents an image using binary.
Starter
Explain to students that data in computers is stored and transmitted as a series of ones and zeros, also referred to as “Binary”.
Display the following simple 1-bit image on the board and ask students to suggest how it could be converted to binary. Try to draw out answers such as "Use 0 to represent white and 1 to represent black" or "Use 0 to represent black and 1 to represent white".
Explain to students that data in computers is stored and transmitted as a series of ones and zeros, also referred to as “Binary”.
Display the following simple 1-bit image on the board and ask students to suggest how it could be converted to binary. Try to draw out answers such as "Use 0 to represent white and 1 to represent black" or "Use 0 to represent black and 1 to represent white".
Alternative Starter
Ask the students to stand in a line and place on the floor (or table) a stack of white and stack of black paper/card (preferably cut into squares). Display the following image on the board / screen (See Binary_Starter.pdf) and explain to the students that each 0 represents a white card and each 1 represents a black card. Instruct students to, in turns, pick up the corresponding coloured card for the next number in the sequence (starting from left to right / top to bottom) and place it in the corresponding position on the floor / table. Inform students that, once they have placed down their card, they must return to the end of the line. (To aid the students, the teacher can cross off each number in the sequence after each turn).
Once the last card has been placed down, display the solution (Binary_Starter.pdf) and compare it to the solution on the floor/table.
Ask the students to stand in a line and place on the floor (or table) a stack of white and stack of black paper/card (preferably cut into squares). Display the following image on the board / screen (See Binary_Starter.pdf) and explain to the students that each 0 represents a white card and each 1 represents a black card. Instruct students to, in turns, pick up the corresponding coloured card for the next number in the sequence (starting from left to right / top to bottom) and place it in the corresponding position on the floor / table. Inform students that, once they have placed down their card, they must return to the end of the line. (To aid the students, the teacher can cross off each number in the sequence after each turn).
Once the last card has been placed down, display the solution (Binary_Starter.pdf) and compare it to the solution on the floor/table.
Starter
| binary_starter_exercise_festive.pdf |
Main
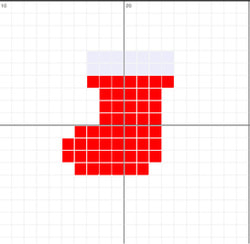
Display the following sequence of images.
Display the following sequence of images.
Explain to students that, in a computer, an image is broken down into tiny elements called pixels and that each pixel (short for picture element) represents one colour. Explain that an image with a resolution of 1024 by 798 pixels has 1024 x 798 pixels (817,152 pixels).
Tell students that, in order for the computer to store the image, each pixel is represented by a binary value (One or Zero). Explain that we call this representation of colours a “bit-plane” and that each bit doubles the number of available colours i.e. 1-bit would give us 2 colours, 2-bits would give us 4 colours and 3-bits would give us 8 colours etc.
Display the following image and ask the students how they think a computer would interpret it using binary? Draw out answers such as: 'Use 00 for white and 11 for black etc.' and 'Use two bits to represent each colour' etc.
Tell students that, in order for the computer to store the image, each pixel is represented by a binary value (One or Zero). Explain that we call this representation of colours a “bit-plane” and that each bit doubles the number of available colours i.e. 1-bit would give us 2 colours, 2-bits would give us 4 colours and 3-bits would give us 8 colours etc.
Display the following image and ask the students how they think a computer would interpret it using binary? Draw out answers such as: 'Use 00 for white and 11 for black etc.' and 'Use two bits to represent each colour' etc.
Show the following example and explain that images are stored in “scan lines” and that each line is encoded from left to right --> top to bottom.
Show students the following image and ask them how they think a computer would represent an image containing 4 colours.
Explain to the students that in an image that uses 4 colours, 2 bits are needed for each pixel. The following example uses two bits to store the following colours:
00 – White; 01 – Black; 10 – Red; 11 – Beige
00 – White; 01 – Black; 10 – Red; 11 – Beige
Explain that we call this representation of colours a “bit-plane” and that each bit doubles the number of available colours i.e. 1-bit would give us 2 colours, 2-bits would give us 4 colours and 3-bits would give us 8 colours etc.
After showing students how a computer would represent a 2 colour and 4 colour image, ask the students to suggest how we could store more colours such as 16, 256 etc.
Inform the students that an image represented by 24-bits would have 16 million colours - 16,777,216 to be precise.
After showing students how a computer would represent a 2 colour and 4 colour image, ask the students to suggest how we could store more colours such as 16, 256 etc.
Inform the students that an image represented by 24-bits would have 16 million colours - 16,777,216 to be precise.
Activity 1 (Unplugged version)
Explain to the students that, in this lesson, they will be creating their own bitmap images and converting these to binary. If necessary, model an example of this on the board - See support worksheet (below) for some examples to model.
Give each student a pre-printed computer science cracker joke, each with a different challenge attached – tasks based on level of ability. (See below). Instruct the students to complete the challenge attached to their cracker joke.
Explain to the students that, in this lesson, they will be creating their own bitmap images and converting these to binary. If necessary, model an example of this on the board - See support worksheet (below) for some examples to model.
Give each student a pre-printed computer science cracker joke, each with a different challenge attached – tasks based on level of ability. (See below). Instruct the students to complete the challenge attached to their cracker joke.
| cracker_jokes.pdf |
| bitmaps-blank.pdf |
| bitmaps-large.pdf |
|
Activity 1 (Digital version)
|
Examples
Plenary
Write the following binary example on the board and ask the students how the computer would interpret the numbers.
101001001001101
Note: You can write any binary number on the board - the idea being for the students to ask questions such as how many colours etc.)
Ask students what does a computer need to know to be able to convert the image. Explain that, in order for the computer to interpret the file, the computer needs to know:
• Colour depth – how many bits represent each pixel
• Resolution - Width & Height (in pixels)
Finally, explain that we call this “metadata”
Write the following binary example on the board and ask the students how the computer would interpret the numbers.
101001001001101
Note: You can write any binary number on the board - the idea being for the students to ask questions such as how many colours etc.)
Ask students what does a computer need to know to be able to convert the image. Explain that, in order for the computer to interpret the file, the computer needs to know:
• Colour depth – how many bits represent each pixel
• Resolution - Width & Height (in pixels)
Finally, explain that we call this “metadata”
Alternative Plenary
Alternatively, finish by recapping the learning objectives using the Pose, Pause, Pounce and Bounce method.
Example:
Pose a question to the whole class e.g. Explain how a 16 colour image can be represented in binary
Pause to give students time to digest the question and think of their answer. If the students are engaged, try holding the pause for a little while longer to build up the tension.
Pounce: Quickly, select a student to answer the question. i.e. Insist the answer to the question comes from student A and possibly student B, directly and fast! Obviously, plan in your mind who you are going to direct the questions to before hand.
Bounce the question or student's response on to another student (immediately after the pounce). e.g. Ask them if they agree with the students previous answer and to explain why.
For more information about the Pose, Pause, Pounce and Bounce technique, visit: @teachertoolkit - https://teachertoolkit.me/2013/01/04/pppb-version2/
Alternatively, finish by recapping the learning objectives using the Pose, Pause, Pounce and Bounce method.
Example:
Pose a question to the whole class e.g. Explain how a 16 colour image can be represented in binary
Pause to give students time to digest the question and think of their answer. If the students are engaged, try holding the pause for a little while longer to build up the tension.
Pounce: Quickly, select a student to answer the question. i.e. Insist the answer to the question comes from student A and possibly student B, directly and fast! Obviously, plan in your mind who you are going to direct the questions to before hand.
Bounce the question or student's response on to another student (immediately after the pounce). e.g. Ask them if they agree with the students previous answer and to explain why.
For more information about the Pose, Pause, Pounce and Bounce technique, visit: @teachertoolkit - https://teachertoolkit.me/2013/01/04/pppb-version2/
Support:
- Share with students some exmaples (see below)
| support.pdf |
Extension:
- Students can share the binary code of their favourite bitmap image with a classmate to see if they could convert it back to the original image.
- Some students can convert their image to hexadecimal (using the help sheets provided below)
| bin2hex.pdf |
Keywords:
Binary, image, resolution, depth, pixels, metadata, colour
Binary Representation of Images (Festive Edition) lesson is licenced under a Creative Commons Attribution 4.0 International License.
Tags: GCSE, KS4, KS3, Theory, Computing Theory, CS Theory, Binary, Binary Representation, binary 2, binary conversion, how to do binary conversion, counting binary, binary number to decimal, binary 101, 8 binary, binary digits, binary digit, meaning of binary